Edge detection

We can use filters to approximate various operations on continuous functions. For example, a possible approximation for a derivative at a point nT for a function f(x) is ${1\over T}(f[n+1] - f[n-1])$Note that this is the convolution of f[n] with ${1\over T}h[n]$ which is defined by

$$h[-1] = 1,\quad h[1] = -1,\quad h[n]=0\ \mbox{for all other n}$$ (3)

Approximations of the derivative can be used to detect edges in a picture.

We can define an edge point as a point where the function f(x) (intensity in the case of images) changes faster than at the points next to it. That means that the derivative f'(x) has a maximum at this point. (We have assumed that the function is differentiable.) Thus we can find the edges of a function by looking at the local maxima of the derivative.

In two dimensions, the analog of the derivative is the gradient vector $( {{ \partial f} \over {\partial x}}, { {\partial f} \over {\partial y}})$. The edges can be defined as points where the magnitude of the gradient is above some threshold.

We approximate the directional derivatives $\partial f \over \partial x$and $\partial f \over \partial y$ in a way similar to (3). To make the method less sensitive to fluctuations in the images, we can average the derivative in perpendicular direction. This leads to the following filter for the horizontal derivative:

$$\left( \begin{array}{rrr} 1 &0 &-1\\ 2 &0 &-2\\ 1 &0 &-1\\ \end{array} \right)$$

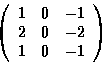
In the matrix above, the center corresponds to h[0,0].

A similar filter can be used for the vertical derivative:

$$\left( \begin{array}{rrr} 1 &2 &1\\ 0 &0 &0\\ -1 &-2 &-1\\ \end{array} \right)$$

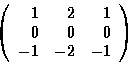
To find the edges in an image, we compute the convolutions with each of these filters and estimate the magnitude of the gradient at each point

$$\sqrt{ \left( {\partial f \over \partial x}\right)^2+ \left({\partial f \over \partial y}\right)^2}$$

.

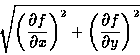
and compare it to he chosen threshold. The choice of threshold depends on the image.