Background

Fourier transform

Frequency domain.

In this section, we will look at how a signal, such as an audio recording or an image, may be broken down into different frequency components. This change in representation is accomplished by the Fourier tranform. The

Spatial frequency.

When we discuss audio signals we typically talk about time frequency, that is, how fast a signal oscillates in time. In the context of antialiased image manipulation, we almost always use ``frequency'' to mean spatial frequency, rather than, for example, the frequency of light waves. Just as the simple harmonic oscillator is a simple case of something with a well-defined frequency of motion, a sine wave grating (Figure 1) is an image with a single, well-defined spatial frequency.

  

Figure 1: Sine-wave grating. The intensity of the image varies as a sine wave.

Angular frequency units.

The unit of frequency that we use in this handout is the radian per unit time or space. For example, if a weel rotates at the rate 1 full rotation per second, the frequency is $2\pi$ radians per second. If a sine wave has period T seconds, the frequency of this wave is $2\pi/T$. When we consider images, the period T is spacial, not temporal, and is measured in suitable units, such as inches or pixels.

One-dimensional signals

We will mostly consider one-dimensional signals-functions of one variable, such as monophonic audio recordings, or a single row of an image. Everything can be easily generalized to two-dimensional signals, such as images.

Fourier transform

The Fourier transform ${\cal F}{[x]}$ of a function x(t) is defined as:

$${\cal F}{[x]}(\omega) = \int_{-\infty}^{\infty} {x(t) e^{-i \omega t}dt}$$

For a given a frequency $\omega$, the Fourier transform ${\cal F}{[x]}(\omega)$ is a complex number c. The magnitude of cindicates how much of the frequency is present, and the $\omega$indicates the phase of that frequency component relative to the origin.

Inverse Fourier transform

The inverse Fourier transform recovers the original signal from its Fourier transform, and is defined as:

$${\cal F}^{-1}{[X]} = {1\over 2\pi} \int_{-\infty}^{\infty} {X(\omega)e^{i\omega t} d\omega}$$

Note that the forward and inverse FTs are almost the same operation. This will be quite convenient when analyzing sampling and filtering.

Examples

The Fourier transforms of the following simple signals will be useful for understanding sampling, shifting and resizing.

Constant function

A constant function k consists of only one frequency-zero. Therefore its Fourier transform $K = {\cal F}{[k]}$must be zero everywhere except at $\omega = 0$.

$$\mbox{ for all $\omega\neq 0$ } ,\quad K(\omega) = 0$$

The value at zero frequency should be selected such that the inverse Fourier transform yields k:

$$k = {1\over 2\pi} \int_{-\infty}^{\infty} {K(\omega)e^{i\omega t} d\omega}$$

To satisfy these two conditions simulteously we need to introduce an unconventional function, the $\delta$-function, which is defined as:

$$\mbox{ for all $x\neq 0$ } ,\quad\delta(x) = 0$$

$$\mbox{ for all $\epsilon$ } ,\quad \int_{-\epsilon}^{+\epsilon}\delta(x) dx = 1$$

Despite its name, it is not a function at all; it is a more general object called distribution. The $\delta$-function can be thought of as an operator that cancels integration: when multiplied by a function appearing inside an integral, it causes the value of the integral to be equal to the value of the function evaluated at a point.

So the Fourier transform $K(\omega)$ of a constant function k is a delta-function at the origin:

$$K(\omega) = 2\pi k\delta(\omega)$$

Box

The box function is defined by:

$$b(t) = \left\{ \begin{array}{ll} 1 & -1/2 \leq t \leq 1/2 \\ 0 & \mbox{otherwise} \\ \end{array} \right.$$

Its Fourier transform, known as the sinc, is given by:

$$B = {\cal F}{[b]} = \int_{-\infty}^{\infty}b(t) e^{-i \omega t}dt$$

$$= \int_{-1/2}^{1/2} e^{-i \omega t}dt$$

$$= {\sin(\omega/2)\over(\omega/2)} = sinc \left( \omega \over 2 \pi \right)$$

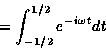
The definition of sinc is

$$sinc(x) = { {\sin{ \pi x}} \over {\pi x}}$$

Comb

The definition of the comb function is:

$$comb = \sum_{n=-\infty}^{\infty} \delta(t-nT)$$

  

Figure 2: The comb function.

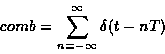
Since this function is periodic, it may be expressed as a Fourier series, and all its frequency content are in a series of harmonics. In fact, its transform is another comb function. Since the period of the original comb was T, the fundamental frequency of its transform will be $2\pi/T$.

$${\cal F}{[comb]} = {{2\pi} \over T} \sum_{n=-\infty}^{\infty} \delta(\omega-(2\pi n/T))$$

The derivation of this fact is relatively complicated and we omit it here. Section 2.3 describes a generalization of the comb function known as the impulse train.

[htb]

Useful properties

Figure 3 summarizes a number of identities involving the Fourier transforms of special types of signals.

Name of the property	signals	Fourier transforms
Linearity	ax(t)+by(t)	$a{\cal F}{[x]}(\omega)+ b{\cal F}{[y]}(\omega)$
Time shifting (Section 3)	x(t-t0)	$e^{-i\omega t_0}{\cal F}{[x]}(\omega)$
Zooming (Section 4.1)	x(t/a)	$a{\cal F}{[x]}(a\omega)$
Differentiation	dx(t)/dt	$i\omega{\cal F}{[\omega]}$
Convolution (Section 2.2)	x(t)*y(t)	${\cal F}{[x]}(\omega){\cal F}{[y]}(\omega)$

 

   
Filtering and convolution

Later in this handout we will describe circumstances in which we want to remove high or low frequencies from images. The frequency domain is a natural place to think of doing this; ideally, we could multiply all the desired frequencies by one and all the unwanted ones by zero. Although strictly speaking such an operation is not possible, we will use it as an idealization throughout this handout.

Linearity and shift invariance

Operations on signals are referred to as filters. A simplified type of filter-linear, shift invariant-turns out to be adequate for our antialiasing purposes. A filter ${\cal L}[s]$ of this class (operating on a signal s) has the following properties:

• Linearity: for signals x, y, and real-valued $\alpha$:

  
  

  $${\cal L}[x + y] = {\cal L}[x] + {\cal L} [y]$$
  
  

  
  

  $${\cal L}[\alpha x] = \alpha {\cal L}[x]$$
  
  

• Shift invariance: if $\hat{x}(t) = x(t - \tau)$ and $\hat{\cal L}(t) = {\cal L}[t - \tau]$, then the following relation holds.

  
  

  $${\cal L}[\hat{x}] = \hat{\cal L}[x]$$
  
  

  i.e. the result of application of a filter to a shifted signal is the shifted version of the result that we get if we apply the same filter to the original signal.

For the rest of this handout we will use ``filter'' only to refer to linear and shift-invariant filters.

Band-pass filtering example

For an example of filtering, consider the analog telephone, which is supposed to transmit audio frequencies in the range of 300 to 3000 Hz. We could represent the sound of a voice on the telephone as:

$$T(\omega) = H(\omega) V(\omega)$$

Where V is the Fourier transform of the original voice, T is the Fourier transform of the voice on the telephone, and His the following frequency response:

$$H(\omega) = \left\{ \begin{array}{ll} 1 & \mbox{if}\;\; 300... ...pi\; \mbox{Hz} \\ 0 & \mbox{otherwise} \end{array} \right.$$

Frequency response; impulse response

A filter, like a signal, may be represented either in the frequency domain, in terms of its frequency response, or in the time domain, by its impulse response. As with a signal, the forward and inverse Fourier transforms convert between representations.

We can express filtering in the time domain rather than the frequency domain as an operation known as convolution. The expression for the convolution on two signals x(t) and y(t) is

$$u(t) = \int_{s=-\infty}^{+\infty} x(s)y(t-s) ds$$

It is usually written u = x*y.

In the frequency domain, filtering is simply multiplication by a function. In the time domain, it becomes convolution. Conversely, multiplication by a function in the time domain becomes convolution in the frequency domain.

Discrete signals

So far we were discussing only continuous signals. If we are going to process our signal digitally, we will have to deal with discrete signals, that is, signals defined only at isolated points. We will consider signals defined at uniformly spaced points of the real line nT, where n is an integer, T is the sampling period. We will use the notation x[n] for such signals.

An important question is how to represent the sampled signal in such a way that we can use the machinery of the Fourier transform. In order to use the continuous Fourier Transform, we need a signal defined on the real line, not on a set of discrete points. The naive approach doesn't work: if we define the signal x_sampled(t)=x[n] at points nT and zero elsewhere, the Fourier integral of this signal will be zero.

It turns out that we can obtain a convenient representation of a discrete signal if we use the comb function. We represent the discrete signal x[n] with

$$\sum_n{ x[n] \delta(t - nT)}$$

Then sampling a continuous function x(t) is equivalent to multiplying x(t)by the comb function x[n] = x(nT) is represented by

$$x(t)\sum_n{ \delta(t - nT)} = \sum_nx(t){ \delta(t - nT)} = \sum_n{x(nT) \delta(t - nT)}$$

We will call a signal represented in this manner an impulse train.  

Intuitively, the impulse train representation can be interpreted as follows: an approximation to a $\delta$-function is a spike of a small width aand the height $1\over a$, with area 1; the area under the plot of a spike can be interpreted as the energy of the spike. If we multiply the spike by a number c, the energy becomes c. Thus, we can think of the impulse trains as idealizations of uniform sequences of spikes with varying energy.

Fourier transform of discrete signals

A reason for using the impulse train representation of discrete signals is that now we can apply the CFT to the signal:

$${\cal F}{[\sum{x[n] \delta(t - nT)} ]} = 2\pi/T \int{\sum{x[... ...lta(t - nT)}} e^{-i \omega t}dt = \sum{x[n] e^{-i \omega nT}}$$ (1)

Alternatively, we could define the FT of a discrete signal to be the sum above. The impulse train allows us to establish a connection between these two types of Fourier transforms.

Note that the FT in Equation 1 is periodic in $\omega$ with period ${2\pi}\over T$, because $e^{-i \omega nT}= e^{-i(\omega+ { {2 \pi} \over T })T}$. That means that we have to consider FT of discrete signals only on the interval $[-\pi/T, \pi/T]$. The number ${2\pi \over T} = \Omega_s$ is called sampling frequency.

We can derive a number of properties of the FT of discrete signals from the properties of the CFT. A list of such properties is shown in the table below.

  

Figure 4: Properties of the Fourier transform of discrete signals

Shannon sampling theorem

An interesting question is when the FT of a continuous signal x(t) coincides with the FT of the discrete signal on $[-\Omega_s/2, \Omega_s/2]$. FT has all the information about the signal, and if we can recover the FT of the continuous signal from the FT of the sampled version, we can recover the continuous signal from the samples exactly.

We can answer this question using the convolution theorem. The sampled signal x_sampled(t) is just the product of the comb function with the continuous function x(t); therefore,

$$\begin{eqnarray*}{\cal F}{[ x_{sampled} ]} = {\cal F}{[x\ comb]}= \frac{1}{2\pi}... ...infty}^{+\infty}{\cal F}{[x]}*{\delta(\omega - k\Omega_s)} &&\\ \end{eqnarray*}$$

As the convolution with $\delta(\omega - k\Omega_s)$ is just a shift by $\Omega_s$, we can see that the Fourier transform of the sampled signal is just a sum of shifted copies of Fourier transforms of the continuous signals:

$${\cal F}{[x_{sampled}]} = \frac{1}{T}\sum_{n = -\infty}^{+\infty}{\cal F}{[x]}(\omega - n\Omega_s)$$

Equation 1 gives a different representation:

$${\cal F}{[x_{sampled}]} = \sum_{n = -\infty}^{+\infty}x[n] e^{-i \omega nT}$$

It is quite remarkable that an infinite sum of shifted copies of the FT of a continuous function turns out to be just a sum of exponents multiplied by discrete samples of the signal.

This fact has some important consequences:

We can immediately see when the FT of the sampled signal coincides with FT of the original signal on $[-\Omega_s/2, \Omega_s/2]$: this happens only when there is no overlap between the shifted copies of ${\cal F}{[x]}$. In particular, there is no overlap if the continuous signal x(t) is band-limited, that is, the Fourier transform of the signal is 0 for all frequencies above some frequency $\Omega_c$. Figure 5 shows that there is no overlap if $\Omega_c< \Omega_s- \Omega_c$, that is, if $\Omega_c< \Omega_s/2$. The frequency $\Omega_s/2$ is called the Nyquist frequency.

  

Figure 5: Sampling

If a signal x(t) is band-limited below the Nyquist frequency, then the Fourier transform of the sampled signal consists of copies of ${\cal F}{[x]}$ centered at $k\Omega_s$; we can use a low-pass filter with cutoff frequency $\Omega_s/2$ to get rid of extra copies. If we use the ideal low pass filter sinc, we will recover the original signal exactly. This result is called Shannon theorem or Nyquist theorem:

Theorem 1 (Shannon,Nyquist)   Let x(t) be a band-limited signal with

$${\cal F}{[x]}(\omega) = 0 \quad \mbox{for}\ \vert\omega\vert > \Omega_c= \Omega_s/2$$

Then x(t) is determined exactly by its samples x[n] = x(nT), where $T = { { 2\pi} \over \Omega_s}$.

We can derive an explicit formula for reconstructing the signal by convolving appropriate sinc function with the sampled function x_s(t) = x(t) comb(t). The signal x(t) can be reconstructed from samples x[n]using

$$x(t) = \sum_{n=-\infty}^{+\infty} x[n]{{ \sin{\pi(t- nT)}/T}\over{\pi(t- nT)}/T}$$

   
Discrete convolution

If we convolve an impulse train $\sum x[n]\delta(t - nT)$ with another impulse train $\sum y[n]\delta(t - nT)$ , the result will be

$$\begin{eqnarray*}\sum_{n,m} x[m] y[n] \delta(t - mT)*\delta(t-nT) = \sum_{n,m}... ...( t - kT) = \sum_k (\sum_{n}{x[k-n]y[n]}) \delta( t - kT) &&\\ \end{eqnarray*}$$

We get a new impulse train which corresponds to a discrete signal

$$(x*y)[k] = \sum_{n}{x[k-n]y[n]}$$ (2)

which is called the discrete convolution of x and y Given that the signals x[n] and y[n] have finite length, this is an operation that we can perform on a computer. As it is just the regular convolution applied to impulse trains, the Convolution Theorem holds:

Theorem 2   If x[n], y[n] are discrete signals and (x*y)[n] is their convolution,

$${\cal F}{[ x*y]} = {\cal F}{[x]}{\cal F}{[y]}$$

Now we have all tools in place for the applications that we are interested in: resampling of a discrete signal at a different set of points and filtering the signal in order to modify its properties.

Sampling and reconstruction pipelines

Sampling

The following pipeline summarizes the process of sampling. Given a sampling rate, Shannon's theorem gives the cutoff frequency of the prefilter h.

  

Figure 6: Sampling

As described above, if the original signal has been passed through an ideal low-pass filter during sampling, then an identical filter h may be used to reconstruct the signal.

  

Figure 7: Reconstruction