projects

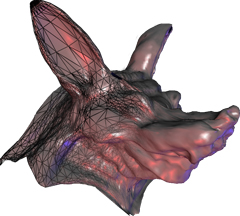
Multiresolution surfaces are a natural extension of subdivision surfaces; in addition to refining a base control mesh using a fixed subdivision rule, details are added at each refinement step. The resulting mesh is a semiregular mesh, that is, most vertices of the mesh have fixed valence (same as for a regular grid), and only few isolated vertices have a different valence. This representation inherits many attractive features and efficiency of subdivision, while allowing one to represent high resolution surface geometry, either constructed from scratch or obtained using a 3D scanner.

One of the crucial advantages of multiresolution surfaces for representing most common high-resolutiuon surfaces comes from the fact that the connectivity of the mesh need not be explicitly stored, except for few extraordinary vertices, just as pixel adjacencies need not be explicit for an image. In most cases, connectivity of a fine mesh approximating a surface is an artifact of a triangulation process, such as marching cubes, and conversion to a semiregular mesh does not result in the loss of geometric information. Regular structure of multiresolution surfaces considerably reduces memory requirements, improves data coherence and allows one to use much more efficient algorithms.

Multiresolution surfaces are closely related to wavelet-based and overcomplete image representations, and more generally, makes surfaces much more similar to images. This makes it possible to generalize many of the signal processing techniques to handle geometric data, with applications in modification, compression and transmission of surface data (surface processing).

Our research in this area includes several directions:

• Multiresolution editing. Our past work on interactive editing of high-complexity surfaces resulted in development of basic tools for multiresolution representations.
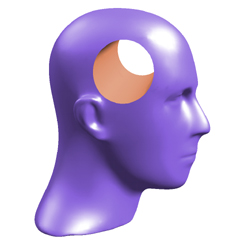
• Approximate boolean operations on multiresolution surfaces. Using unions, intersections and differences is a natural way of constructing more complex objects out of primitives. Free-form boundary representations using NURBS or subdivision surfaces are not closed under these operations; the result can be only approximated. Multiresolution surfaces are well suited for computing such approximate results of boolean operations with any desired precision. A more detailed description and examples are available on a separate page.
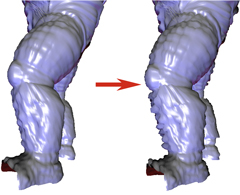
• Surface processing. We aim to generalize a variety of filters used for images to the case of multiresoltion surfaces and develop new filters for automatic surface modification. A first step in this direction is our work on surface denoising.

More information coming soon!

People

• Henning Biermann
• Daniel Kristjansson
• Lexing Ying
• Jianbo Peng
• Vasily Strela
• Denis Zorin

Publications

Procedural Shape Synthesis on Subdivision Surfaces

Luiz Velho, Ken Perlin, Lexing Ying, Henning Biermann

Proc. SIBGRAPI 2001.

Sharp features on Multiresolution Subdivision Surfaces

Henning Biermann, Ioana M. Martin, Denis Zorin, Fausto Bernardini

Proc. Pacific Graphics 2001.

Texture and Shape Synthesis on Surfaces

Lexing Ying, Aaron Hertzmann, Henning Biermann, Denis Zorin

Proc. 12th Eurographics Workshop on Rendering, Jun 2001.

Boolean Operations on Free-form Solids

Henning Biermann, Daniel Kristjansson, Denis Zorin

Proc. SIGGRAPH 2001.

Interactive multiresolution mesh editing

D. Zorin, P. Schröder, W. Sweldens

Computer Graphics (SIGGRAPH '97 Proceedings), pp. 256-268.

Subdivision and Multiresolution Surfaces

Denis Zorin

Ph.D. Thesis, Caltech, 1998.