Texture mapping from images
One way to impart a lot of realism or just interesting detail to a computer graphics scene is to map some color variation from an image onto your 3D objects.
In order to map an image onto an object in your scene, you need to compute, for each visible pixel where you can see the object, which pixel of the image maps onto that point. This operation generally takes place as part of the pixel shader.
If you are doing zbuffer rendering, then this will take place once per pixel during scan-conversion of a triangle. On the other hand, if you are ray tracing, then this will take place each time a nearest ray/surface intersection is found.
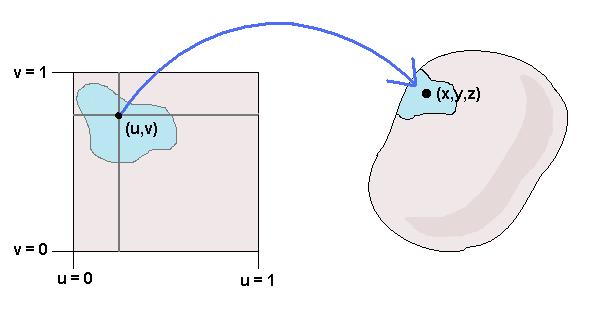
Given a point on an object, you need to figure out where to look up in the source image. To make this process easier, we generally adopt the following convention: Whatever the resolution of the source image, locations on the source image are described by a pair of floating point coordinates (u,v), where 0 ≤ u ≤ 1 and 0 ≤ v ≤ 1, as in the diagram.

In the diagram the arrow goes from the image source location (u,v) to the object surface point (x,y,z), because this is the way we generally think of the texture mapping as being from an image to a 3D object. But in practice we actually need to compute the inverse function: While we are rendering the scene we have a point (x,y,z) on an object's surface, and we need to go from there to a location (u,v) in a texture source image.
There are a number of ways to define this inverse mapping function f: (x,y,z) → (u,v). One general set of techniques is referred to as projection mapping, so called because it consiste of some way of "projecting" down from a three dimensional space to a two dimensional space. Which type of projection to use depends upon the shape of the object you want to texture.
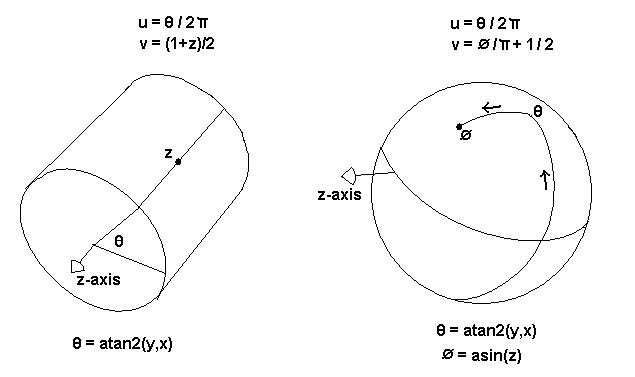
For example, if you have a roughly cylindrical object (such as an arm or a tree trunk or a can of soup), you might want to do cylindrical projection mapping: f: (x,y,z) → ( atan2(y,x) / 2π, (1+z)/2 )
Similarly, if you have a roughly spherical object you might want to do spherical projection mapping: f: (x,y,z) → ( atan2(y,x) / 2π , asin(z)/π + 1/2 )
Of course before you do any of these mappings, you can first do a matrix transformation, so that your texture space is properly scaled and centered on the object. The complete sequence of transformations is thus:
Loading in the image:
Of course, in order to do texture mapping you need a source image, and you need to be able to read individual r,g,b pixels of that source image. But that's not really computer graphics, that's just plumbing. I've provided a Java class that handles this plumbing for you:
ImageBuffer: A java class to support loading an image
Antialiasing:
If the object you are texturing is visibly small in the scene, then you will encounter a case where a single pixel of the output image coresponds to many pixels in the source texture image.
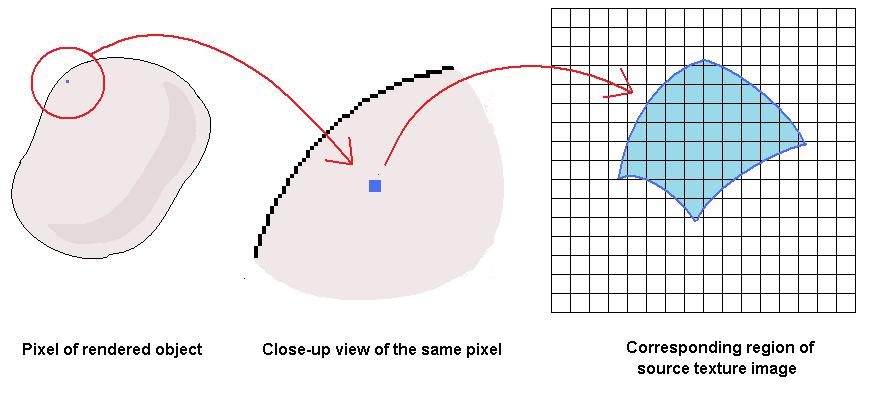
As we discussed in class, if you just grab the value at a single pixel of the source texture image, then in such cases you will end up undersampling the source texture image, which will result in visible artifacts. To deal with this, you need some way of approximating the integral over an entire region of the source texture image. A number of methods of providing a quick and reasonably accurate approximation to this integral have been developed over the years. We are going to focus on one that was developed by Lance William in the early 1980s known as "MIP Mapping".
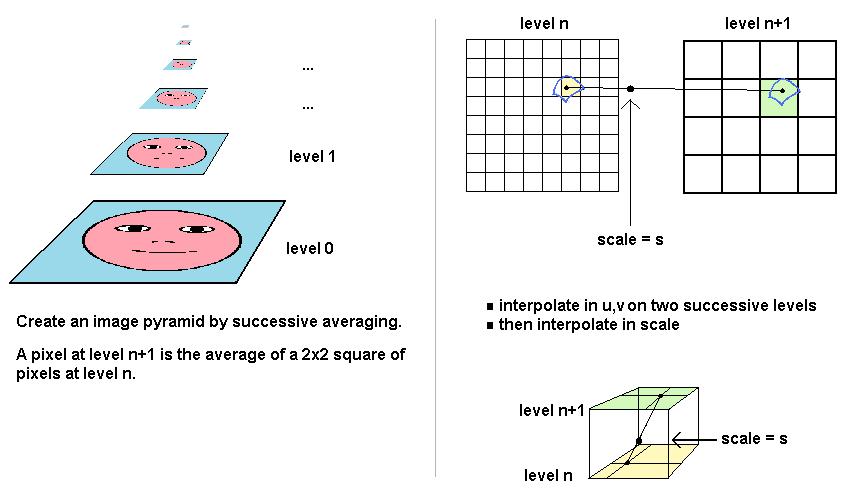
The basic principle of MIP Mapping is that you preprocess the texture source image into an "image pyramid". This pyramid consists of a sequence of images, where image n+1 is half the resolution in each dimension as image n. Each pixel (i,j) in image n+1 contains the averaged values of pixels (2i,2j), (2i+1,2j), (2i,2j+1), (2i+1,2j+1) from image n.
Procedural texturing
For the lecture on procedural texturing, everything you need to go over the principles and then try your own experiments is at the following links:
Try to take the ideas (and your own creative variations of the ideas) implementated in that last link, to incorporate procedural textures into your own Z-buffer renderer or ray tracer.
What do you do with the texture values?
Actually, you don't need to use texture values just for color variation. You can apply texture to any operation in your shader. For example, if you are using a Phong shader, you can use the texture values to vary the power of the specular component of your surface shader.